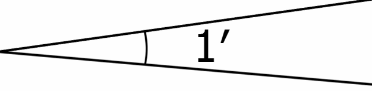Foreword
This book stems from many years of discussion and tireless introduction of measurement and inspection technology to those in industry responsible for the control of product quality. It became clear that there are few outside of the quality profession who understand and appreciate the measurement process, its implications and its techniques. I hope that through the use of this primer there can be a better understanding of what it takes to “take a measurement”.
MEASUREMENT
By:
Richard G. Chitos
What is measurement?
By Richard G Chitos- Willrich Precision Instrument Company, Inc
Chapter 1
Measurement- (Latin mensura) A figure, extent or amount obtained.
We are surrounded by measurement. Almost everything we do involves measurement of some kind. We measure the distances we run, the mileage we reveal to work each morning, the ingredients of a cake, and the scores on our kid’s report cards. Just because it’s not a manufactured product doesn’t mean that measurement is not taking place. Sometimes we use perceptive measurements such as “Tom’s nose is too big for his face” or “Betty is surely built well”. Whether you realize it you’ve taken measurement mentally. Unlike the “2000-year-old man” I can’t say when all of this measurement got started. It probably all began when man began.
You’ve heard some stories about how we arrived at some very popular units of measurement. You know the stuff about the king’s foot being considered a standard measurement so “Presto!’ We get the standard foot. Unfortunately, the standard holds up for only a particular king’s foot; obviously this proved to be a rather poor measurement standard. Some other standards have been, the width of a thumb for an inch, the distance from the nose to the outstretched arm as a value of a yard etc. It seems those many years ago there was quite a hang-up on various body parts.
Measurement came into its own when groups of men were needed to build things. A solidarity artisan making a piece of pottery dealt with his individual perception of the size or volume of his work. But when it came to using hundreds and sometimes thousands of workers for time periods that could last for a hundred years or more, measurement and standards became essential. Can you imagine building the pyramids, the Parthenon or the Great Wall of China without some hard and fast rules and regulations. Although individual design plate it’s role, individual standards could not be tolerated. Henry Ford heralded the modern production line and the interchangeability of parts, yet it is obvious that these concepts had to be understood by those master builders of old.
Thousands of years ago in Egypt units of measurement known as “cubits” were used. The cubit was based on the length of the forearm from the elbow to the tip of the middle finger. (Here’s that hang-up on body parts again). What is important is that standards are established. If a number of stones were needed two cubits by three cubits by two cubits, the first of these was made and designed as a standard, to which all others could be compared. Here we have the birth of comparative measurements. A principle that has stayed with us for thousands of years. It’s clear in today’s world we can’t walk around dragging a bunch of standards behind us, but we can readily obtain and uses tools that have been compared to a standard somewhere.
Just as our culture, its drama art and architecture is based on the works and the thinking of those great masters in the distant past, so does our ability to make reliable and meaningful measurements have its beginnings way back when. Had Euclid, and Pythagoras been busy thinking other thoughts we would not be able to accomplish much today. The old adage says “if you can’t measure it you can’t make it”. Few, if any high schoolers, as they suffer through their geometry classes can appreciate the implication and application of what they are being taught. I can appreciate this better than most as I had to take the subject twice and it surely wasn’t because I was enamored with its principles.
Without measurement we can neither produce or progress. You certainly could not produce a toaster or an automobile, that has thousands of parts without knowing that “this will go into that.” The designers of whatever is being produced demand that their specifications are met so that the finished product meets their ideal of fit, form, and function. That is that it performs its intended job. When the various parts of an assembly are designed there is included very specific instructions as to the materials to be used, the processes required and the nominal sizes of features along with the tolerances applied to those features. Tolerances are the amounts that the features of the apart are allowed to deviate from the perfect or ideal. No process is so exact that in our attempt to manufacture parts that we can make them 100 percent perfect. Tolerances recognize that there is going to be variations. Tolerances allow for some variation that will still permit the product to function.
Measurements are critical to all products. It is clear that parts of the space shuttle require some very critical measurements be taken. However, to the maker of chewing gum the thickness of the gum may be equally important. Make the gum too thick and the pieces won’t fit in their intended package, too thin and they’ll rattle around in the package. Besides, government regulations require that packages of consumer goods meet the package weights indicated. Too thin a product could lower the package weight and be construed as consumer fraud. Making the product purposefully thicker leads us back to the package problem again, but also increases the cost of raw materials. Giving away just a few grams of product on each package, when one could possibly be producing billions of packages, could equate to hundreds of thousands of dollars of additional costs.
In the beginning…………………………………………………………………………………….
Every product starts with an idea. Some gizmo or widget is needed to fill a need. The burden of designing these gizmos and widgets is given to the design engineers who come up with the plans to build the product. We can think of their specifications as the laws that need to be followed to assure product performance. These laws could be likened to the laws created by our legislative branch of government (the congress and the senate) their laws (specifications) are transmitted to the executive branch (the president) in the hopes that they will be carried out as congress intended, just as our design engineers pass on their “laws” to production to carry out the requirements to produce the product. And just as in our government something is sure to go wrong in the process, there is a need for judges to define if the law of the land is being observed, so it is true that judged are required in industry. Quality inspectors confirm or deny that the desired design specifications have been met. The similarity stops, in that generally inspectors are not asked to interpret the laws necessarily but to pass in the adherence of them (although every seasoned inspection professional has certainly done his or her share of interpreting).
So, just as our forefathers created a system of checks and balances in our government similar checks and balances are used in industry. These checks and balances can often times be aborted by having those responsible for quality inspection reporting to supervisors in the production group. That is why supreme court justices are appointed for life. They needn’t fear that their decisions will affect their positions. Maybe this is a call for guaranteed job security for the inspection department?
More and better products have to be made in order to secure our standard of living and that of the rest of the world. Greater productivity and quality products will secure America’s position as a world leader. Metrology- The science of measurement can help us reach those goals.
Nominal- The basic size
Tolerance- The amount the feature is allowed to vary from the perfect or ideal
Gizmo- Gadget
Widget- An unnamed article considered for purposes of hypothetical example
If .001 is “one thousandths” then 10 of them have to be… you got it! “Ten thousandths”.
If we see the value .010” we know we are ten times greater than .001”
Moving right along, if we multiply ten times ten we get one hundred likewise .010” x 10 = .100” or “one hundred thousandths”.
If we double any of these values the rules remain the same, the value just doubles.
.001” x 2 = .002” – – “Two thousandths”
.010” x 2 = .020” – – “Twenty thousandths”
.100” x 2 = .200” – – “Two hundred thousandths”
Remember now that the third place after the decimal is the starting place. In one of our examples we had shown the fraction 7/16 to be .4375” hey, that’s a fourth place after the decimal. Now the rules change a bit.
The fourth place is expressed as the “tenths” position. Why? Because it is ten times smaller than the “thousandths” place. It is “one tenth of a thousandths”.
.0001” is 1” divided up 10,000 times.
.0001” is 1/10,000
.0001” is .001/10
.0001” x 10,000 = 1”
Five of these little buggers (.0005”) is expressed as “five- tenths of a thousandths”.
Getting back to our example .4375” is therefore expressed as “four hundred thirty-seven thousandths and five tenth thousandths”.
In shop talk in order to shorten this mouthful a bit the value is sometimes referred to as “four hundred thirty-seven thou and five tenths”.
Most of you may want to stop here for those who need to or who are just curious the trek continues.
There is a fifth, sixth, seventh, etc. place after the decimal. For our purposes we’ll deal with the 5th and 6th places, so expression of the value doesn’t become too cumbersome.
Let’s look at a real wild number. .437532”. All the rules for the first part of the number remain unchanged (.4375) what changes is the last part. Instead of deferring to the popularity of the “thousandths” position a new position reign supreme “the millionths position”. Which is the sixth position after the decimal place (.000001).
.000001 x 1,000,000 = 1”
.000001” = One millionth
Guess what? Ten of these are ten millionths .000010”. Getting back to expressing the value we say .437532” is “four hundred thirty-seven thousandths and thirty two millionths”. Quite a mouthful, but sometimes necessary. In some cases, the millionth or ten millionths place is referred to in scientific notation.
1 x 10-6 equals .000001” One millionth
2 x 10-6 equals .000002” Two millionths
1 x 10-5 equals .000010” Ten millionths
2 x 10-5 equals .000020” Twenty millionths
For the first example all you need to do is take 1 consider there is a decimal place assumed after the number (1.) then move the decimal, in this case six times.
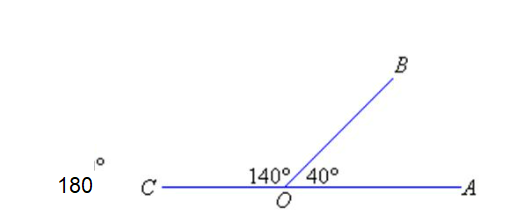
Angles on Angles
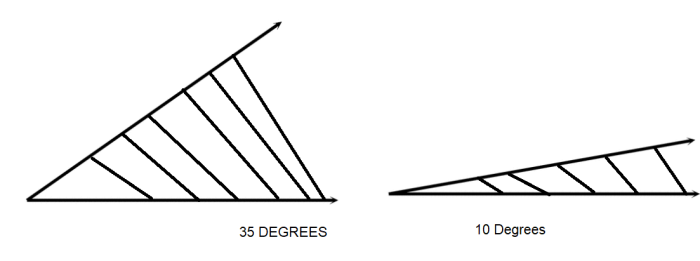
Any circle can be broken into 360 parts (degree). No matter how big or small the circle, you can get the same number of pieces from a pie no matter how big or small it is, the only difference is the size of the slice’s changes. As you have heard each of these parts is called a degree. Now, just as we have seen before units of measurement can be broken into smaller and smaller units. Just as hours in the day can be broken into minutes so can degrees. There are 60 minutes in a degree which is a breeze to remember. The next step is to chop these minutes down even further. The next step down is seconds. There are 60 seconds in a minute. Not so tough?
If you sliced a pie every 90 degrees, you’d get 4 slices. Every 45 degrees and you’d have 8 slices (typical with pizza pies). Taking it further, half that or 22 degrees 30 minutes would yield you 16 slices. And so on until you could (if you slice very carefully) wind up with 1,296,000 slices each one being 1 second (360 degrees x 60 minutes x 60 seconds=1,296,000 seconds). An arc is a part of the periphery of a circle and looks like this – – – – – – –
So, when we refer to the parts of this circle we’ve been dissecting we call them “arcs”. So, 90 degrees becomes 90 degrees of arc, and looks like this – – – – – –
45 degrees would be 45 degrees arc, and looks like this – – – – –
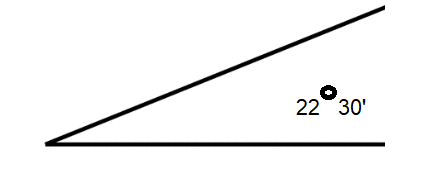
22 degrees, 30 minutes (22 and a half degrees) looks like this – – – – –
1 second of arc (the smallest we’ll ever deal with) could look like this – – – – –
Of course, the larger the circle the larger the arc. A circle going around the waist of the earth (the equator) is 25,000 miles around (periphery), and 1 second of arc would be approximately 102 feet.
How we arrived at this is fairly simple. (25,000 miles divided by 1,296,000 seconds=.0192 miles. There are 5280 feet in a mile so, 5280 x .092 = 101.8 feet).
Therefore, large circles have large arcs and small circles have smaller ones.
If you were driving a car up a steep incline the steeper the incline the steeper the incline the sooner you’d reach the top of the hill. That means for every degree increase in steepness greater heights are achieved. Here’s an example.
Therefore, a relationship exists between angles and linear measurement. If we shot an arrow at the moon and we were off in our aim by 1 second of arc we would miss it by more than a mile. (Boy, those little seconds can sure get in the way). 1 minute over an inch length has a rise of .000291”. The same 1 minute over 10 inches rises from a plane .002909” and over 1 foot the rise is .00341”.
I like to remember that 1 second has a rise of .000005” over 1 inch, this way it’s easy to multiply to get other values. Here’s one for you.
What’s the rise of 2 seconds of arc over 10 inches.
.000005” x 2 = .000010” x 10 = .0001” Approx.
It’s approximate because the value for 1 second is not exactly .000005” but really .00000484” (see chart) though not exact it sure is close enough for most applications.
As you can see in the chart the conversion goes both ways that is linear measurements can be readily changed into angular ones.
You may be thinking how is this done. Actually the conversions are done using trigonometry. Pages through define the process of conversion.
Ok, you’re ready, using the chart as a guide convert 15 seconds over 10 inches into linear measurement.
Next which is greater 22 degrees 15 minutes 10 seconds or 22 degrees 17 minutes 59 seconds?
Linear: Relating to, consisting of, a line: straight
Answers to questions page
- .000727”
- 22^ 17 59”
The manner in which these angles are expressed on a print is again similar to how we express time. Minutes are followed by a ’ and seconds by a ”. The change comes when we express degrees but then again another similarity exists this time between angular degrees and temperature degrees both are expressed using a bubble (o).
Putting this all together we can use the following example to get some practice.
15 o 7’ 42” is actually 15 degrees, 7 minutes, 42 seconds.
Recently there has been a trend to express parts of a degree in decimals. 45 degrees 30 minutes then becomes 45.500 degrees. We divided 30 minutes by 60 minutes and got .500
45 o 20’ would therefore become 45.3 o
45 o 59’ is the 45.98333 or almost 46 o
22 o 59’ 59” which is just a second shy of 23 degrees therefore 22.0031 o
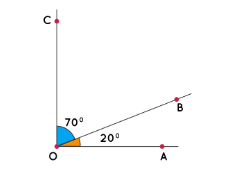
If a full circle has 360 degrees then a semi-circle has 180 degrees. The supplement of an angle is the amount by which an arc or an angle falls short of 180 ^.
SUPLLEMENTAL 40 Deg
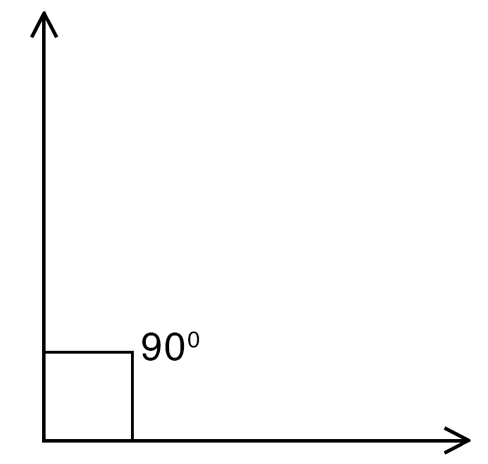
Continuing along the same thought a complement is the amount by which an arc or an angle falls short of 90 ^.
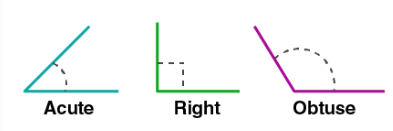
Finally, angles can be right, acute, or obtuse. As per the following examples.
If you’re starting now to feel somewhat obtuse yourself, about angles it’s time to go on to the next chapter.
Accuracy, Resolution, Repeatability
I used to own one of those digital watches which told me the time of day to one tenth of a second. Then one day I realized it didn’t matter very much to me whether I was doing whatever I was doing at 3:15 or 3:15:1?42. So, I bought one of those European looking models that has a graduation every five minutes. I still tell time but not as closely as I used to.
Both watches are very accurate it’s just that with my current one I’ve got lousy resolution. Now I can tell that it’s approx. 3:15 give or take a minute or so. So, what’s suffered? Certainly not the accuracy but rather the resolution – that is the least significant digit that can be read, the digital watch had a LSD of .1 giving it as wristwatches go a high order of resolution. I’m measuring resolutions typically start of mechanical gages having resolutions of .001” (one thous) down to (.00001”) or lower. Don’t confuse resolution with accuracy. I could of course have a watch that resolves to .1 seconds but be “off” by hours. Accuracy is the difference read on the measuring device as it is? being compared to a standard. In the case of the watch the question is what time I do have as compared to the standard which is ticking away in Greenwich England, if it’s exactly the same time I’m accurate if I’m “off” some amount that’s my level of accuracy or inaccuracy – now I’m pretty sure my new watch is accurate but I’ve got a problem. It’s resolution is so coarse that I’ve no way of reading it. Determine how close or “off” I am from the standard.
Lesson #1- It doesn’t pay to have a lot of high accuracy in a gaging system if you’re no way of confirming it. By high resolution now just let’s say my watch is “off: by a full minute = what if I could better its resolution by placing grads on the face every 30 seconds. Now I’ve got lots of resolution, but the watch is still inaccurate. Because the resolution is better, I can see the inaccuracy better but it sure hasn’t helped make the time correct.
Lesson #2- Higher resolution doesn’t buy you much except higher resolution. Accuracy stands alone + hazed? Now what if I check the same watch every day + at the same time + one day it’s running a minute late and the next day it’s exactly on time. The problem we are then facing is one of repeatability. The watch that is a minute off but accurate can be set to the correct time and stay that way, but the one that fails to repeat leaves us with a problem which to reckon.
Lesson #3- I’d rather have a system that is off that I can reset than one that varies all over the place.
Lesson #4- You can never be more accurate than you are repeatable.
Metrology: Distance between two points
Millimeter: Thousands of a meter
Tenths – Micron = Millionth of a meter
Inch – Micron = Million of an inch
Microinch much smaller than micron
Tenth = 100 Microinch
Micron = .004 (HAIR)= .0001 HAIR (.004) = Microinch
————— ——————
40 4000
1 Micron = 40 Millionths
7 Microns = 280 Millionths
.1 Micron = 4 Millionths
20 Microinches = 20 Millionths
4 Microinch = 1 Micron
2 Microinches = .5 Micron
Variable Gage Study
The number of operators (2 or 3) and the number of trials (2 or 3) may vary. Each operator measures 3 – 10 parts in random order for each trial. Data storage is optional. An option of tests are described:
- Gage Repeatability and Reproducibility
Gage repeatability is the variation in measurements obtained when one operator uses the same gage for measuring identical characteristics of the same parts; reproducibility is the variation in the average of measurements made by different operators using the same gage when measuring identical characteristics of the same parts. For each trial, have each operator measure parts in random order. Repeat the cycle, with the parts measured in another random order, for the number of trials required.
- Gage Accuracy
Gage accuracy is the difference between the observed average of measurements and the true average. Establishing the true average is best determined by measuring with the most accurate measuring equipment. Have one operator measure the same parts, using the gage being evaluated.
- Gage Stability
Gage stability refers to the difference in the average of at least two sets of measurements obtained with the same gage on the same parts taken at different times. How gage stability is determined depends on how often the gage is used between normal calibrations. If a gage is used intermittently, then have the gage calibrated before and after each trial to determine the amount of calibration change. If a gage is used constantly, then conduct another gage R&R study.
- Gage Linearity
Gage linearity is the difference in the accuracy values through the expected operating range. Conduct two accuracy studies, one at each end of the operating range.
TYPES OF GAGES
REVERSIBLE WIRE TYPE PLUG GAGES
A wire type plug gage is a plug gage comprising a gaging member of straight cylindrical section throughout its length held in a collect-type handle. This design is standard in the range above .030 to and including .760 inches. DU-WELL offers this type of gage up to 1.010. Sizes below .030 are available on requested note.
TAPERLOCK PLUG GAGE
A taperlock plug gage is a plug gage in which the gaging member has a taper shank, which is forced into a taper hole in the handle. This design is standard for plug gages in the range above .059 to and including 1.510 inches. DU-WELL offers taperlock gages in this range.
TRILOCK PLUG GAGE
A reversible or trilock plug gage is a plug gage in which three wedge-shaped locking prongs in the handle are engaged with corresponding locking grooves in the gaging member by means of a single through screw, thus providing a self-centering support with a positive lock.This design is standard for all plug gages in the range above 1.510 and including 8.010. DU-WELL shows up to 4.010 in the catalogue and will quote prices on larger sizes.
PROGRESSIVE SETTING DISCS
A master setting disc is a cylinder provided with insulating grips, used for setting comparators, snap gages, etc. There are three styles. Style 1 is a plain cylinder approximately twice the length of Style 3. The gagemakers’ tolerance is split plus-minus from the nominal size. Style 2 is two cylinders each approximately one-half the length of the cylinder in Style 1. Generally one cylinder is the “GO” master and the other the “NOT GO”. The gagemakers’ tolerance on the “GO” is minus and on the “NOT GO” it is plus. Style 3 is a plain cylinder approximately one half the length of Style 1. The gag makers’ tolerance is split plus-minus from the nominal size. The standard shows four designs – one for the range .105 to .365, one for .365 to 1.510, one for 1.510 to 2.510, and one for 2.510 to 8.010. DU-WELL lists size ranges for each of the three styles from .150 to 4.510, and will quote on sizes smaller and larger upon request.
PLAIN RING GAGES
A plain ring gage is an external gage of circular form employed for the size control of external diameters. In the smaller sizes it may consist of a gage body into which is pressed a bushing, the latter being accurately finished to size for gaging purposes. This design is optional in the range above .059 to and including .510 inches. Gages in sizes above 1.510 inches are flanged in order to eliminate unnecessary weight and to facilitate handling. An annular groove is provided in the periphery of the “NOT GO” ring gage as a means of identification.
SWIPE
(A lesson in Gage Repeatability and Reproducibility)
BY R.G. CHITOS
There used to be an old rule of thumb that if given a part’s total tolerance the gage selected to measure the part should have a resolution of 10% of the total part tolerance. Until recently no formal mention was made to this method. Today Gage R&R (Repeatability and Reproducibility) tolerances are specified when ordering gaging inspection systems, as well as when applying these instruments to various production inspection tasks. The former method of purely relying on resolution made no provision for gage repeatability, gage accuracy or operator influence. Gage R&R methods and supporting formulas make an effort to resolve the issue by considering all of these variables.
The move to Gage R&R practice is welcome as it finally addresses some of the important areas that all good gaging practitioners have always known. The shortfall is that many of those who interpret the Gage R&R results do not fully understand the results. When specifying a 10% R&R, that is that the result of the test shows that the application of the specific gage tested does not consume more than 10% of the part’s total tolerance, many fail to realize that given standard practices and budgets 10% is not readily achievable. Many Inspection Managers will readily accept results of 20% of the tolerance and even 30% in some cases.
It is surprising how many companies have no idea what percentage of their total tolerance is being “eaten” by poor gages and poorer gaging practice. Routinely, when finally analyzed, gages and their application have consumed 50-60 and 100% of a parts tolerance.
The methods used to perform Gage R&R studies employ the use of several operators to take repeated readings on gaging masters as well as finished parts. The procedures allow for separation of operator reproducibility from gage error. This divides the blame, but in reality the gage supplier is generally saddled with the full brunt of the lack of adherence to the desired specification without regard to all of the variables that affect the final outcome. The very term GAGE R&R places the blame for whatever the problem directly on the gage.
SWIPE
Swipe is a mnemonic which stands for the following influencers of total measurement performance:
S- The Standard, is it certified and when, is it the proper class. For example in setting a bore gage to gage a 1” hole having a .00005” Bandwidth tolerance, if one were to use a class Y tolerance master, the uncertainty of the master alone could be as much as .0001” which is 20% of the total tolerance of the hole to begin with. The roundness of the master may be up to .00005” which is already 10% of the Gage R&R.
W- The Workpiece, every part varies, some more than others. Are the R&R operators aware of the variation within a part? Does the part have intrinsic taper, out of roundness conditions, surface finish variations etc. that can affect the measurements. Just by not taking measurements in the same place or zone on the part repeatedly can cause the R&R to suffer significantly. A .0001” out of roundness condition can consume 20% of the total part tolerance using the example above.
I- The Instrument itself obviously has linearity, and repeatability characteristics. Whatever they may be, clearly they add to the gaging uncertainty. In addition, certain instruments are more prone to operator loading, use, and care.
P- The Personnel and their ability to adapt the gage to the part is an ever important factor. Surely the gages vulnerability to operator influence can be considered the gage’s fault. However one should not discount the variation in touch and experiment that the operator brings to these tests. With some operators and their influence there may be no gages or inspection equipment made to perform the measuring task at hand. Surely an enigma, but best handled when best understood.
E- The Environment. Parts that are dirty, oily, or hot or even cold are poor candidates for R&R testing methods. They may represent the real world conditions but offer no stable ground on which to buyoff on a gages ability.
So there you have it, the SWIPE scenario. The answer may very well be that considering all of the variables, the only one that can be rectified is the gage’s intrinsic accuracy and repeatability. In this case it becomes necessary to obtain gages of a higher order. This may mean changing from Mechanically applied hand tools to Electronic or Air Gage tooling. These tools permit higher resolution and linearity and repeatability. They limit operator influence and offer output to SPC and signaling modules. The cost may increase but the value per item measured makes these types of tools irreplaceable.
Gage R&R, while an important measure in the measure of the measurement system requires careful consideration in its application.